Introduction¶
This project deals with the software realization of one of the most elementary
algebraic operation, the inner product. The first objective is to compute the
inner product as accurate as possible without violating the second objective to
do it as efficient as possible for middle and large dimension vector lengths.
Hereby middle dimension describes vectors with about 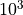 elements and
accordingly large dimension vectors with more than
elements and
accordingly large dimension vectors with more than 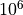 elements.
[1]
elements.
[1]
The inner product is the basis for a large number of numerical applications and computations that are performed using binary floating-point arithmetic on computers. Therefore in Chapter Binary floating-point arithmetic this floating-point arithmetic, specified by the IEEE, is introduced. One part of this specification are the rounding modes, that are examined in detail. Furthermore methods are presented to efficiently extract the exponent part of a binary64. Another part of the IEEE specification is the FMA instruction. This instruction is one of the main reasons for this project, as it becomes available as hardware realization for upcoming generations of consumer processors. The FMA instruction itself and the usage from the programming languages C and C++ are analyzed comprehensively in Chapter The Fused-Multiply-Add operation.
Computing accurate inner products is strongly connected to computing accurate sums, which are treated in Chapter Accurate summation. In this chapter some previous approaches and basic concepts are presented, followed by the introduction of the new algorithm BucketSum for accurate summation. In Chapter Accurate inner product many of the summation approaches are advanced in order to compute accurate inner products. Especially BucketSum is extended to BucketDotProd and FMAWrapperDotProd. Both algorithms exploit the features of the FMA instruction. In this chapter it is shown, that other algorithms benefit from the existence of a hardware version of FMA as well. All presented algorithms are therefore tested numerically using a benchmark program for summation and inner products in the corresponding chapters. The test system for the benchmark programs is described in Appendix Test system information. Finally, the results are concluded in Chapter Conclusion with a perspective for the future.
Footnotes
| [1] | Note that a vector with 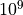 binary64 elements would
almost completely fill the whole 8 GB of main memory of a state of the
art computer system. binary64 elements would
almost completely fill the whole 8 GB of main memory of a state of the
art computer system. |