The Fused-Multiply-Add operation¶

IEEE 754-2008 standardizes the new operation FMA [IEEE-754-2008] (Definition 2.1.28). This operation will be supported by hardware in upcoming CPU instruction sets from AMD [1] [Hollingsworth2012] and Intel [2] [Meghana2013], which at the time of writing are two market leading CPU manufactures. What makes this instruction so attractive is, that it performs two floating-point operations in a single step [3], which can be beneficial for speeding up algorithms. A short history excerpt and a very comprehensive analysis of various algorithms using the FMA operation can be found in [Brisebarre2010] (Chapter 5).

Specification¶

This section deals with how FMA is specified by IEEE 754-2008. Quoting the standard:

“The operation fusedMultiplyAdd(x, y, z) computes (x · y ) + z as if with unbounded range and precision, rounding only once to the destination format.”

—[IEEE-754-2008] (Definition 2.1.28)

FMA¶

function [s] = FMA (a, b, c)
  s = fl((a * b) + c);
end

The property, that the result of the FMA operation is only rounded once in the end, is very important. First of all, one is able to write algorithms that can rely on this property of no intermediate rounding like it would happen if (x · y ) + z is evaluated by two floating-point operations. But on the other hand the programmer has to take care for compiler optimizations. For example an expression like a · b + x · y might be contracted to FMA(a, b, x · y) and any assumptions about intermediate rounding are falsified [Brisebarre2010] (Chapter 7.2). More on the compiler settings for correct usage for FMA follows in the Section Software and compiler support.

Hardware realization¶

At the time of writing the FMA operation is not a fully adopted by all common used computer architectures. Thus, it is important to check if the used system uses a hardware implemented FMA operation in order to avoid slow software emulations as the C11 standard remarks [ISO-IEC-9899-2011] (Chapter 7.12).

Since the year 1990 the FMA instruction has been supported by several processors, like the HP/Intel Itanium, which has been used as testing system by many algorithm implementors in the past [Brisebarre2010] (Chapter 5). For examples see [Ogita2005] and [Graillat2007]. These processors are mainly used for scientific or business applications, but the focus of this project are more common used processor architectures like the Intel 64 and AMD64 [4] architectures, which are mainly compatible with each other. AMD assures that “[…] floating-point operations comply with the IEEE-754 standard.” [AMD2013] (Chapter 1.1.5), as Intel does for FMA too [Intel2015] (Chapter 14.5). So it is assumed, that there is no violation of IEEE 754-2008 on hardware level.

x87 FPU and mapped MMX registers.

AVX packed double addition VADDPD ymm1, ymm2, ymm3/m256.

For analyzing the FMA operation on hardware level, a deeper understanding of the floating-point instruction sets and used registers is required. With this knowledge one can later check on the assembly level, if the “real” FMA is used. Many currently available and all upcoming Intel 64 and AMD64 CPU s support four floating-point instruction sets:

x87 FPU : This instruction set is designed for scalar IEEE 754-1985 floating-point operations on eight separate 80 bit FPU data registers. These registers are used as a stack, to avoid long opcodes. The mnemonics are prefixed by an “F” (float), for example FADD ST(0),ST(i) is such an instruction. ST(x) is the stack pointer to some FPU data register x. The shown instruction replaces ST(0) with ST(0) + ST(i). An urgent problem with these instructions arises from the 80 bit long registers and when, due to execution optimization, floating-point operands are kept in the registers for more than one operation. This problem of “double rounding” is described in [Brisebarre2010] (Chapters 3.3.1). For more information about the x87 FPU, see [Intel2015] (Chapter 8) and [AMD2013] (Chapter 6).
MMX and 3DNow! [5] : In contrast to the x87 FPU instruction set, this one is intended for SIMD operations. Intel supports only integer data types, whereas AMD introduced the extension 3DNow! for supporting floating-point data types as well. This instruction set makes use of eight 64 bit MMX data registers that are mapped onto the FPU data registers (see Figure x87 FPU and mapped MMX registers.). So instead of having two scalar operands for an instruction, MMX allows to operate on so called packed values, which are vectors of some data type (see Figure AVX packed double addition VADDPD ymm1, ymm2, ymm3/m256.). For AMD only, the mnemonics are prefixed with “PF” (packed float), for example PFADD mmx1, mmx2/mem64 would add the packed values from two MMX data registers and store the results in the first operand register. Due to the 64 bit limitation, only two packed single precision floating-point types could be used, see [AMD2013d] (p. 94). See also [Intel2015] (Chapter 9) and [AMD2013] (Chapter 5).
Legacy SSE [6]: To legacy SSE belong SSE1, SSE2, SSE3, SSSE3, SSE4, SSE4.1, SSE4.2, and SSE4A. All these instruction sets are subsequent extensions with new instructions. The difference to MMX is that SSE instructions can operate on both MMX (thus FPU) data registers and eight to sixteen 128 bit XMM data registers depending on enabled 64 bit mode. The packed value concept stays the same as in MMX, but offers more operands at the same time and the support of floating-point types. An example for adding two packed double precision floating-point types is ADDPD xmm1, xmm2/mem128, like with PFADD the result is stored in the first operand register [AMD2013c] (p. 23). The instruction suffix “SD” thus indicates a scalar double-precision operation and the suffix “PD” a packed double operation. More in [Intel2015] (Chapters 10-12) and [AMD2013] (Chapter 4).
Extended SSE: This instruction set is of major interest, as it contains the FMA operation. To extended SSE belongs the AVX instruction set, that offers 256 bit versions of all legacy SSE instructions and further extensions, that are manufacturer depended and not considered. Sixteen 256 bit YMM data registers, whose 128 lower bits are used as XMM data registers (see Figure SSE registers.) are required to perform these extended operations. The mnemonics are prefixed by “V” (VEX-prefix) [Intel2015] (Chapter 14.1.3). There is one important difference between Intel and AMD. Both will have support for the so called FMA 3 operation, but only AMD will support the FMA 4 operation. For the double precision data type FMA 3 will be realized in three versions whose mnemonics are VFMADD132PD, VFMADD213PD, and VFMADD231PD. The numbers 1, 2, and 3 indicate which registers will be multiplied and added [Lomont2011]. The hardware realized FMA 3 operation finally looks for example like this: VFMADD132PD ymm0, ymm1, ymm2/m256. The computation performed is ymm0 = (ymm0 × ymm2) + ymm1. AMDs FMA 4 has the form VFMADDPD ymm1, ymm2, ymm3, ymm4/mem256. This operation is non-destructive, that means, that no operand will be overwritten and remain available for further operations. ymm1 = (ymm2 × ymm3) + ymm4. [Intel2015] (Chapter 14) and [AMD2013c] (Chapter 1).

SSE registers.

AMD64 already offers the FMA 3 operation in processors based upon the microarchitectures “Bulldozer” and “Piledriver”. The latter one supports the FMA 4 operation as well [Hollingsworth2012]. The AVX instruction set, including FMA 3, will be part of Intels fourth generation Core(TM) processors with the code name “Haswell” [Meghana2013].

With this background of floating-point instruction sets it is possible to determine the availability of FMA on a specific system. The CPUID operation is very helpful to get information about AMD or Intel processors. Calling CPUID returns a bit pattern that contains all information about the CPU features. The meanings of the individual bits are described in [AMD2013b] (Appendix E) for AMD or for Intel in [Intel2015a] (Chapter 3.2). Additionally Intel provides an assembler pseudo code [Intel2015] (Chapter 14.5.3) to check the availability of FMA.

Software and compiler support¶

The compiler used in this project is the GCC, a free software compiler, and it’s C++ front end G++. As the manual suggest, the compiler names GCC and G++ can be used interchangeably for C++ source file input [Stallman2015] (Chapter 1). GCC links C programs against the GLIBC [7] and C++ programs are linked against the LIBSTDC++. Using GCC guarantees easy reproducibility of this work. It follows a discussion which options have to be passed to the GCC compiler to fulfill the following three properties:

compliance with the standards C11 or C++11 and IEEE 754-2008
optimized code
enabling the FMA operation by hardware

To fulfill the first property GCC offers the options -std=c11 or -std=c++11 respectively and -pedantic [Stallman2015] (Chapter 2). But GCC is not fully compliant to IEEE 754-2008, C11, and C++11, as online documents state [8] . As long as this issue hasn’t been fixed, it is up to the programmer to carefully check the IEEE 754-2008 conformance. The first case where one gets in touch with the broken implementation is the contracted expression, described earlier for FMA. The C11 standard allows to control the usage of these expression with the FP_CONTRACT pragma [ISO-IEC-9899-2011] (Chapter 7.12.2) [IEEE-754-2008] (Annex F.6). According to the GCC manual this pragma is currently not implemented. But contracting expressions is only enabled, if the -funsafe-math-optimizations or -ffast-math options are used [Stallman2015] (Chapter 4.6). There are two other switches to archive standard compliance. The first one is -fexcess-precision=standard ensuring that “double rounding” (see section Hardware realization) cannot occur as all casts and assignments are rounded to their semantic type, regardless of being stored in for example an 80 bit register. This option is enabled by default, if -std is used. The last one is -frounding-math that disables the optimization assumption of the default rounding mode. Doing this, the currently active rounding mode is respected. One drawback is, that -frounding-math is marked as experimental for the current version [Stallman2015] (Chapter 3.10).

When optimizing software, there is a trade-off between universality, means that the resulting binaries run on a wide range of architectures and machines, and the best possible optimization for one specific machine. As in this work the new FMA operation should be used, all optimization decisions are made to primarily work best on the used test system (see Appendix Test system information). Now that the second and third properties are more hardware depended, they can be examined together. GCC offers the option -O which allows to generically enable four levels of optimization (0-3). The GCC manual states, that even the highest optimization level -O3 does not invoke any options that are in conflict with the first targeted property of standard compliance [Stallman2015] (Chapter 3.10). Thus it is possible to use -O3 safely. GCC also offers many options to enable or disable machine specific features and operations. To overcome the big effort of checking all feature options for applicability, there is the option -march=native that detects all available features of the local machine and enables the feature options accordingly [Stallman2015] (Chapter 3.17.53). Because of this the FMA options -mfma and -mfma4 are enabled too. This fulfills the third desired target. All performed optimizations by the compiler can be inspected using the option -fopt-info to ensure no undesired optimizations were applied [Stallman2015] (Chapter 3.10).

Checking the processor feature bits, like it was done in Section Hardware realization, only gives the information, that FMA is available on a system. It does not guarantee, that the compiled program makes use of that operation by hardware. To prove the latter, two steps are suggested. The first one is to prove the specified property of single rounding is held. The second one is to inspect the compiled assembler code to find the FMA instruction. A test case for the single rounding property is given in the Appendix FMA test cases. This test case considers any rounding mode. An excerpt of the implementation of the first FMA test case for 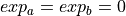$exp_{a} = exp_{b} = 0$ is given in Listing Excerpts of the FMA test case 1 implementation. These test case programs could verify, that only the hardware FMA instruction delivers the desired results.

A very short excerpt of the compiled program from Listing Excerpts of the FMA test case 1 implementation for roundTowardNegative is given in Listing Excerpt from test_1_fma_rd.s. Indeed, the FMA 4 operation (vfmaddsd) and an instance of the FMA 3 operation (vfmadd231sd) are used in the form of a scalar double-precision operation, because of the “sd” suffix [AMD2013c] (Chapter 2). Even if compiled with the highest optimization level -O3, it is not possible to use packed double-precision operations, due to data dependencies in the program of Listing Excerpts of the FMA test case 1 implementation. But for this test program this circumstance is of minor interest.

Performance¶

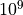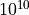With being able to use the FMA operation it is now interesting to compare the performance to other basic operations. The benchmark program simply repeats an operation on a given amount of data. To be more precise, an outer loop increases the number of repetitions, in this case ten steps from $10^{9}$ to $10^{10}$ repetitions. This is done to see how the operation scales compared to others. The most important excerpts of the benchmark program are in Listing Excerpt from benchmark_fma.cpp. A look in the compiled routines (Listings Excerpt from benchmark_fma_1.s, Excerpt from benchmark_add_1.s and Excerpt from benchmark_mult_1.s) reveals, that the repeated floating-point operation is performed in a scalar and serial way, indicated by the “sd” suffix, like described in Section Hardware realization. Additionally the code parallelization by a technique called “partial loop unrolling” [AMD2014] (Chapters 3.4 and 8.2) is taken into account by the benchmark program. Basically this technique means nothing more than to repeat the code for a distinct and independent memory location, e.g. var[i] and var[i + 1]. Independent means, that var[i] is not computed from var[i + 1] in a preceding floating-point operation. Partial loop unrolling violates the well-known Don’t Repeat Yourself design principle, but it allows the compiler to make relaxed assumptions about instruction reordering and register usage. This allows to perform more floating-point operations per clock cycle, thus the instruction-level parallelism increases [AMD2014] (Chapters 3.4 and 8.2). The compiled version of the parallelized benchmark program is shown in Listing Excerpt from benchmark_fma_4.s. A further step would be to make use of packed value (“pd”) operations, but later in the proposed algorithms these instructions cannot be used, due to data dependencies and thus it is not considered in the benchmark program. The results of the benchmark program for five levels of parallelism are shown in Figure FMA performance compared to addition and multiplication..

FMA performance compared to addition and multiplication.

The results of this benchmark program verify, that the pure FMA operation is as fast as a simple addition and multiplication for AMD “Piledriver” CPU s. The same result was taken by another benchmark as well [Fog2014] (p. 64). The reason for the equal results is the usage of the same floating-point multiply/add subunit for all of these operations [Fog2014] (p. 53 and 64). Thus FMA can be used as a hardware implemented operation without having any performance penalties.

Footnotes

[1]	Advanced Micro Devices, Inc.

[2]	Intel Corporation

[3]	This does not necessarily mean a single CPU clock cycle.

[4]	Also known as AMD x86-64.

[5]	Instruction set introduced by AMD.

[6]	Terms “legacy SSE ” and “extended SSE ” are adopted from [AMD2013] (Chapter 4.1.2).

[7]	Note that Ubuntu 13.10 uses http://www.eglibc.org/, which is based upon GLIBC .

[8]	See http://gcc.gnu.org/c99status.html and http://gcc.gnu.org/onlinedocs/libstdc++/manual/status.html .