Binary floating-point arithmetic¶
This chapter is a short introduction to the used notation and important aspects of the binary floating-point arithmetic as defined in the most recent IEEE 754-2008. A more comprehensive introduction, including non-binary floating-point arithmetic, is given in [Brisebarre2010] (Chapters 2 and 3).
Notation and encoding¶
In this project only the binary 64 bit floating-point format is regarded. In
the floating-point standard it is called binary64. The C and C++ data
type double realize this format as well, see [ISO-IEC-9899-2011] (Annex F)
and [ISO-IEC-14882-2011] (Chapter 18.3). The set of normal and subnormal
binary64 floating-point numbers 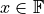 is defined by
the precision p = 53 and the exponent constant E = 1023.
is defined by
the precision p = 53 and the exponent constant E = 1023.
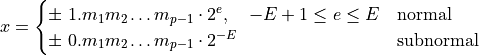
Next to normal and subnormal numbers, a binary64 can take the special
values 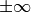 and NaN [Brisebarre2010] (Chapter 3). For this
project the binary64 encoding plays an important role, e.g. for the
exponent extraction (see Chapter Fast exponent extraction). This
encoding is shown in Figure Encoding of a binary64 floating-point number. with the most significant sign bit, an eleven bit exponent and a 52 bit
significant [IEEE-754-2008] (Chapter 3.4).
and NaN [Brisebarre2010] (Chapter 3). For this
project the binary64 encoding plays an important role, e.g. for the
exponent extraction (see Chapter Fast exponent extraction). This
encoding is shown in Figure Encoding of a binary64 floating-point number. with the most significant sign bit, an eleven bit exponent and a 52 bit
significant [IEEE-754-2008] (Chapter 3.4).
Encoding of a binary64 floating-point number.
To get an idea of the range of binary64 numbers, some useful macro constants of the double data type from the C standard library header <float.h> [ISO-IEC-9899-2011] (Chapter 5.2.4.2.2) are listed in Table Some double macro constants from <float.h>.
| Marco name | Value | Description |
|---|---|---|
| DBL_MIN | 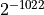 |
Smallest positive normal number |
| DBL_TRUE_MIN | 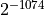 |
Smalles positive subnormal number |
| DBL_MAX | 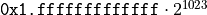 |
Largest positive normal number |
| DBL_EPSILON | 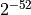 |
Relative unit roundoff |
Rounding¶
IEEE 754-2008 requires the results of conforming floating-point
operations to be correctly rounded, see Definition 2.1.12 and Chapter 9 in
[IEEE-754-2008]. The following description is a brief summary of
[Brisebarre2010] (Chapter 2.2) to explain a correctly rounded floating-point
number in the context of a given rounding mode. Assume a general positive,
normalized, binary, infinite precise floating-point number 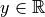 . Then the first p bits are the representable bits (remember for
binary64 the precision p is 53), followed by a rounding bit and the
remaining bits results in the sticky bit. The sticky bit is set, if any bit of
. Then the first p bits are the representable bits (remember for
binary64 the precision p is 53), followed by a rounding bit and the
remaining bits results in the sticky bit. The sticky bit is set, if any bit of
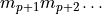 is set.
is set.
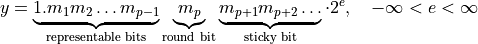
In order to be representable as binary64, y has to be rounded to a
floating-point number 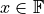 . This rounding operation will be
defined by the function x = fl(y). The result of fl() is dependent on
the active rounding mode. The IEEE 754-2008 specifies the following
rounding modes:
. This rounding operation will be
defined by the function x = fl(y). The result of fl() is dependent on
the active rounding mode. The IEEE 754-2008 specifies the following
rounding modes:
- roundToNearest
- roundTiesToEven
- roundTiesToAway
- roundTowardPositive
- roundTowardNegative
- roundTowardZero
For a binary IEEE 754-2008 implementation roundTiesToEven is the
default rounding mode, though the other three rounding modes have to be
implemented as well, see Chapter 4.3.3 [IEEE-754-2008]. Depending on the sign
of y, roundTowardZero behaves like roundTowardPositive or
roundTowardNegative respectively. This rounding mode will be neglected in the
following examinations. Table Comparison of rounding modes (according
to [Brisebarre2010], Chapter 2.2.1) gives an overview how the different
rounding modes work. “-” indicates that the significant of y is simply
truncated after 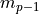 . “p” means that
. “p” means that 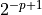 has to be added
to the significant, that is truncated after bit
has to be added
to the significant, that is truncated after bit 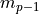 .
.
| round bit | sticky bit | roundTowardNegative | roundTowardPositive | roundTiesToEven |
|---|---|---|---|---|
| 0 | 0 | – | – | – |
| 0 | 1 | – | p | – |
| 1 | 0 | – | p | – |
| 1 | 1 | – | p | p |
Thus an infinite precise result of an arithmetic operation y is correctly rounded according to a rounding mode, if the rules above are applied. This definition is intangible for mathematical proofs on error estimations of floating-point operations. To overcome this problem, several measures have been introduced. The first one is the relative unit roundoff ε, especially for binary64 holds ε = DBL_EPSILON. With this measure a correctly rounded result x = fl(y) according to [Brisebarre2010] (Chapter 2.2.3) can be defined as:
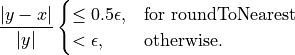
This more intuitive measure for the term correctly rounded means, that for any rounding mode the relative error should be smaller than the representable bits of the rounded floating-point result x. Additionally for roundToNearest the relative error can be maximal exactly the tie value 0.5 · ε (the round bit of y), or is “one bit smaller” than for any other rounding mode.
A measure for the absolute error is the unit in the last place
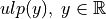 , which is defined for any real number in
[Brisebarre2010] (Definition 5) as:
, which is defined for any real number in
[Brisebarre2010] (Definition 5) as:
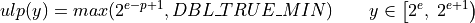
ε and ulp(y) are related via ulp(1) = ε, see [Brisebarre2010] (Chapter
2.6.4). Roughly spoken, ulp(x), 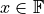 is the significance
of bit
is the significance
of bit 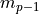 of x or reciting the original definition:
of x or reciting the original definition:
“ulp(x) is the gap between the two floating-point numbers nearest to x, even if x is one of them.”
—[Brisebarre2010] (p. 32)
When there is a unit in the last place, it seems likely that there exists a unit in the first place as well. Rump, Ogita, and Oishi introduce ufp(y) in [Ogita2008]:
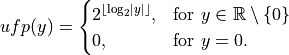
Both ε and ufp(y) are often found in literature about error analysis of floating-point algorithms in various forms and have some weaknesses in their informative value. Discussions about the limitations can be found in [Brisebarre2010] (Chapter 2) and with emphasis on ufp(y) in [Rump2012].
Fast exponent extraction¶
A crucial operation for the later proposed algorithms is to extract the exponent of a binary64. The standard C library offers two functions to extract the exponent part, namely frexp() and ilogb(), see [ISO-IEC-9899-2011] (Chapter 7.12.6) and [ISO-IEC-14882-2011] (Chapter 26.8) for details. Additionally two more hardware dependent methods were tested too. The first of these is to define a data structure, that allows to conveniently view certain bit positions of a binary64 as unsigned integers, see Listing Exponent extraction via type conversion. This approach has also been chosen for the algorithm implementations in [Hayes2010]. As done in the last line of Listing Exponent extraction via type conversion, the binary64 has to be cast to the structure in order to extract the exponent. This approach is called “bit ops” in Figure Exponent extraction performance compared to the add operation. as it performs operations on the bit level representation of the binary64.
1 2 3 4 5 6 7 8 9 10 11 | typedef struct { unsigned mantissa_low:32; unsigned mantissa_high:20; unsigned exponent:11; unsigned sign:1; } ieee754_double; /* ... */ double d = 1.0; unsigned exponent = ((ieee754_double *) &d)->exponent; |
The last considered approach is to use inline assembly to directly call the assembler instruction fxtract wrapped by a function with an interface similar to that one of frexp(), see Listing Exponent extraction via inline assembly.
1 2 3 4 5 6 7 8 | inline double asm_fxtract (const double input, int *exponent) { double result = 0.0; double exp = 0.0; __asm__ ("fxtract": "=t" (result), "=u" (exp):"0" (input)); *exponent = (int) exp; return result; } |
To compare these four approaches for extracting the exponent of a binary64, a small benchmark program has been created. The benchmark program performs the extraction operation on a varying number of input operands and repeats for each number of operands the action 100 times. This has been done to receive measurable results, as this operation is performed too fast to obtain reliable results for a small amount of input. The timings of the four methods have been compared relative to the time needed by a simple addition operation on the same amount of input data, as visible in Figure Exponent extraction performance compared to the add operation.. The choice of the addition operation as reference value is not deciding. Figure Exponent extraction performance compared to the add operation. reveals almost equal timings for the multiplication operation. Because of this, the multiplication plot is hidden behind the addition plot in Figure Exponent extraction performance compared to the add operation.. A final remark on the benchmark program is the instruction-level parallelism. The benchmark was performed with one to four parallel instructions by a technique called “partial loop unrolling”, which is explained later in Chapter Performance.
Figure Exponent extraction performance compared to the add operation. shows, that type casting (“bit ops”) performs best for extracting the exponent and might have been chosen intentionally for the algorithm implementations in [Hayes2010]. Even for the parallel case this approach doesn’t perform worse than an addition or multiplication operation, what is beneficial if one is able to parallelise this task for the input data. One drawback of this approach is, that like the assembler instruction fxtract, it is hardware depended. Thus a user of the presented algorithms has to take care for the data structure of Listing Exponent extraction via type conversion to be applicable to his machine. If the user favours generality over performance, the standard library function frexp() should be chosen for the task of exponent extraction.
Exponent extraction performance compared to the add operation.