Appendix¶

Test system information¶

The test system used for this project is described in this chapter.

Software¶

Software properties of the test system¶
Property	Value
Operating system	Ubuntu 13.10
Linux kernel version	3.11
Compiler	gcc 4.8.1
C library	eglibc 2.17

Linux commands to verify the system software properties¶

# kernel information
uname -a

# compiler and C library information
gcc --version
ldd --version

Hardware¶

Hardware properties of the test system Taken from http://h10025.www1.hp.com/ewfrf/wc/document?docname=c03550353&lc=en¶
Property	Value
Notebook name	HP g6-2239eg
Microprocessor	2.3 GHz AMD Quad-Core A10-4600M APU with Radeon HD 7660G/7670M Dual Graphics
Microarchitecture	Piledriver [Youngbauer2012]
Chipset	AMD A70M FCH
Microprocessor Cache	4 MB L2 cache
Memory	8 GB DDR3

Linux commands to verify the system hardware properties¶

# CPU information
cat /proc/cpuinfo
dmidecode -t processor

# memory information
free -b
dmidecode -t memory

FMA test cases¶

Mathematical description of the first FMA test case:

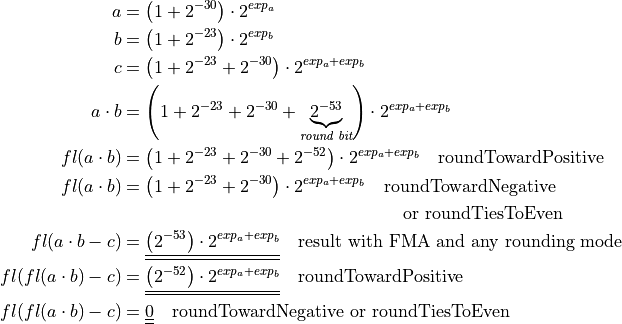
$\begin{aligned} a &= \left(1 + 2^{-30}\right) \cdot 2^{exp_{a}} \\ b &= \left(1 + 2^{-23}\right) \cdot 2^{exp_{b}} \\ c &= \left(1 + 2^{-23} + 2^{-30}\right) \cdot 2^{exp_{a} + exp_{b}} \\ a \cdot b &= \left(1 + 2^{-23} + 2^{-30} + \underbrace{2^{-53}}_{\textit{round bit}}\right) \cdot 2^{exp_{a} + exp_{b}} \\ fl(a \cdot b) &= \left(1 + 2^{-23} + 2^{-30} + 2^{-52}\right) \cdot 2^{exp_{a} + exp_{b}} \quad\text{roundTowardPositive} \\ fl(a \cdot b) &= \left(1 + 2^{-23} + 2^{-30}\right) \cdot 2^{exp_{a} + exp_{b}} \quad\text{roundTowardNegative} \\ & \hspace*{6,5cm}\text{or roundTiesToEven} \\ fl(a \cdot b - c) &= \underline{\underline{\left(2^{-53}\right) \cdot 2^{exp_{a} + exp_{b}}}} \quad\text{result with FMA and any rounding mode} \\ fl(fl(a \cdot b) - c) &= \underline{\underline{\left(2^{-52}\right) \cdot 2^{exp_{a} + exp_{b}}}} \quad\text{roundTowardPositive} \\ fl(fl(a \cdot b) - c) &= \underline{\underline{0}} \quad\text{roundTowardNegative or roundTiesToEven} \end{aligned}$

Mathematical description of the second FMA test case:

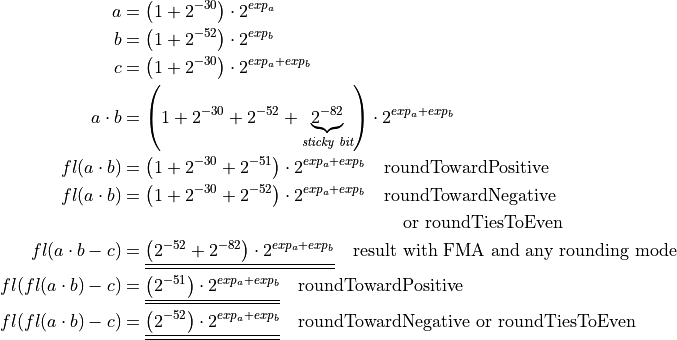
$\begin{aligned} a &= \left(1 + 2^{-30}\right) \cdot 2^{exp_{a}} \\ b &= \left(1 + 2^{-52}\right) \cdot 2^{exp_{b}} \\ c &= \left(1 + 2^{-30}\right) \cdot 2^{exp_{a} + exp_{b}} \\ a \cdot b &= \left(1 + 2^{-30} + 2^{-52} + \underbrace{2^{-82}}_{\textit{sticky bit}}\right) \cdot 2^{exp_{a} + exp_{b}} \\ fl(a \cdot b) &= \left(1 + 2^{-30} + 2^{-51}\right) \cdot 2^{exp_{a} + exp_{b}} \quad\text{roundTowardPositive} \\ fl(a \cdot b) &= \left(1 + 2^{-30} + 2^{-52}\right) \cdot 2^{exp_{a} + exp_{b}} \quad\text{roundTowardNegative} \\ & \hspace*{6,5cm}\text{or roundTiesToEven} \\ fl(a \cdot b - c) &= \underline{\underline{\left(2^{-52} + 2^{-82}\right) \cdot 2^{exp_{a} + exp_{b}}}} \quad\text{result with FMA and any rounding mode} \\ fl(fl(a \cdot b) - c) &= \underline{\underline{\left(2^{-51}\right) \cdot 2^{exp_{a} + exp_{b}}}} \quad\text{roundTowardPositive} \\ fl(fl(a \cdot b) - c) &= \underline{\underline{\left(2^{-52}\right) \cdot 2^{exp_{a} + exp_{b}}}} \quad\text{roundTowardNegative or roundTiesToEven} \end{aligned}$

Excerpts of the FMA test case 1 implementation¶

/* ... */

double x = 1.0 + std::pow (2.0, -30.0);
double y = 1.0 + std::pow (2.0, -23.0);
double z = -(1.0 + std::pow (2.0, -23.0) + std::pow (2.0, -30.0));
#if !defined(NO_FMA)
  double expect = std::pow (2.0, -53.0);
#elif (ROUNDING_MODE == FE_UPWARD)
  double expect = std::pow (2.0, -52.0);
#else
  double expect = 0.0;
#endif

/* ... */

// Try to set rounding mode
int error = std::fesetround (ROUNDING_MODE);

/* ... */

// Initialize data
for (int i = 0; i < DATA_LENGTH; i++) {
  v1[i] = x;
  v2[i] = y;
  v3[i] = z;
}
for (int i = 0; i < PARALLEL; i++) {
  a[i] = 0.0;
}

/* ... */

a[0] += std::fma (v1[j], v2[j], v3[j]);

/* ... */

a[0] += (v1[j] * v2[j]) + v3[j];

/* ... */

Excerpt from test_1_fma_rd.s¶

.L15:
     # ...
     vfmaddsd    (%r12), %xmm5, %xmm4, %xmm2 # *v3_20, tmp107, tmp106, D.37327
     vfmadd231sd 8(%rbx), %xmm6, %xmm1       # MEM[(double*)v2_18 + 8B], tmp108, D.37327

FMA benchmark program¶

Excerpt from benchmark_fma.cpp¶

/* ... */

clock_t t_start = clock ();

// inner loop: several computation
for (long j = 0; j < i; j += PARALLEL) {

/* ... */

#if defined(BENCHMARK_FMA)
  c[0] = std::fma (a, b, c[0]);
#if PARALLEL > 1
  c[1] = std::fma (a, b, c[1]);

/* ... */

#if defined(BENCHMARK_ADD)
  c[0] += a;
#if PARALLEL > 1
  c[1] += a;

/* ... */

#if defined(BENCHMARK_MULT)
  c[0] *= a;
#if PARALLEL > 1
  c[1] *= a;

/* ... */

}

/* ... */

  clock_t t_end = clock ();

/* ... */

Excerpt from benchmark_fma_1.s¶

.L10:
     incq        %rdx                 # j
     vfmadd231sd %xmm2, %xmm3, %xmm1  # b, a, c$
     cmpq        %rbx, %rdx           # i, j
     jl          .L10                 #,

Excerpt from benchmark_add_1.s¶

.L10:
     incq   %rdx                 # j
     vaddsd %xmm2, %xmm1, %xmm1  # a, c$, c$
     cmpq   %rbx, %rdx           # i, j
     jl     .L10                 #,

Excerpt from benchmark_mult_1.s¶

.L10:
     incq   %rdx                # j
     vmulsd %xmm2, %xmm1, %xmm1 # a, c$, c$
     cmpq   %rbx, %rdx          # i, j
     jl     .L10                #,

Excerpt from benchmark_fma_4.s¶

.L10:
     addq        $4, %rdx            #, j
     vfmadd231sd %xmm1, %xmm2, %xmm3 # b, a, c$0
     cmpq        %rbx, %rdx          # i, j
     vfmadd231sd %xmm1, %xmm2, %xmm4 # b, a, c$1
     vfmadd231sd %xmm1, %xmm2, %xmm5 # b, a, c$2
     vfmadd231sd %xmm1, %xmm2, %xmm0 # b, a, c$3
     jl          .L10                #,

Bucket visualizations¶

This appendix is intended to give a visual impression of the bucket alignment and the accumulation process. Therefore each figure contains an orange number line, that indicates for each column the bit significance as a power of two and as a biased exponent representation according to the binary64 format. 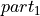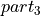The accumulation buckets are visualized as 53 bit arrays, labelled a, with two white leading bits, a green accumulation reserve $part_{1}$ , two white guard bits, a red shift and finally a blue $part_{3}$ , see Chapter BucketSum. Each bucket is aligned to the orange number line with a shift of 18 bits. For exceptional buckets in the over- and underflow-range the colors have the same meaning, as for “normal” buckets, only Acc[113] in Figure Visualization of the bucket alignment in the overflow range. is initialized with NaN and thus colorless.

Figures Visualization of the bucket alignment in the underflow range. and Visualization of the bucket alignment in the overflow range. show how the utmost buckets differ from the “normal” ones in the inner exponent range. These figures are intended to help with understanding the limitations of BucketSum.

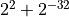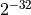Figure Visualization of the stress test case for roundToNearest. shows the worst case summation example for the buckets Acc[56] and Acc[54] when using roundToNearest. The worst case addend here is $2^{2} + 2^{-32}$ , which is exactly the tie value of this rounding mode and the only value, that results in an error of magnitude $2^{-32}$ in this case. This accumulation error of bucket Acc[56] is visualized as red 53 bit array and shows the necessity of the guard bits.

Figure Visualization of the stress test case for roundTowardNegative. shows the same scenario for roundTowardNegative and its worst case addend 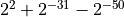$2^{2} + 2^{-31} - 2^{-50}$ . The maximal possible error for this rounding mode is almost twice of that one from roundToNearest. The necessity of the guard bits becomes clear as well.

Visualization of the bucket alignment in the underflow range.

Visualization of the bucket alignment in the overflow range.

Visualization of the stress test case for roundToNearest.

Visualization of the stress test case for roundTowardNegative.