Conclusion¶

In this chapter the results of the previous chapters should be summarized. After giving the reader an overview about binary floating-point arithmetic in Chapter Binary floating-point arithmetic, an efficient way of extracting the exponent part of a binary64 was described by using bit operations. The standard library functions did not provide the desired performance. A very desirable future development would be, that a successive version of IEEE 754-2008 addresses this feature. Then hardware vendors need to provide a high speed function on hardware level. The existing fxtract, is slower than simple bit level operations, as it has to extract the significant part additionally and that there do not exist vectorized versions of it. In Chapter The Fused-Multiply-Add operation it was shown, that the upcoming hardware supported FMA instruction performs as like as other arithmetic operations and that all features of IEEE 754-2008, especially the rounding property, are given. For the FMA instruction the desired development, first a specification, then a very efficient hardware realization, already happened.

The Chapters Accurate summation and Accurate inner product were dedicated to the development of the efficient and accurate summation algorithm BucketSum and its extension to an inner product algorithm BucketDotProd. After giving the reader an overview of the respective operation, it was shown, that computing the inner product is closely related to summation via the property of error-free product transformation. All algorithm implementations of these chapters try to make as much use of the given system features as possible. For example techniques like partial loop unrolling make more use of the processor pipeline, compiling with the flag -march=native enables the usage of AVX and FMA instructions, if available. But the presented algorithms are not perfect in any case. Depending on the system and the used data format and the data lengths themselves, parameters of the partitioning might have been chosen differently to for example increase the accumulation reserve. Therefore the description of BucketSum was intended to be as generic as possible to enable a fast adaptation to different environments. Chapter Accurate inner product also shows, that a new hardware implemented function can result in a huge gain of performance for many existing algorithms, that were considered to be too expensive, if the operation has to be emulated by other basic floating-point operations. As a representative example, TwoProduct could be reduced from 17 FLOP s to two. This makes error-free product transformation more interesting for other applications. The realization of a more ambitious demand by Kulish [Kulisch2013] (Chapter 8), to even fully implement the accurate sum and inner product by hardware, would be interesting for the future as well. But as long as these operations are not standardized, no hardware vendor might be interested in such a realization.

The application field of the presented algorithms is quite large, as summation and inner products are very elementary operations. Possible future works might use these algorithms for verified computations or to tune their parameters to be extended to whole matrix operations, like for example the residual computation for iterative methods. The residual computation

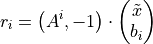
$r_{i} = \left( A^{i}, -1 \right) \cdot \begin{pmatrix} \tilde{x} \\ b_{i} \end{pmatrix}$

is basically nothing more than a matrix-vector product and thus several inner product computations. All in all dealing with elementary operations offers many possibilities to tie in with further works.